Memahami Sifat-Sifat Dasar Aliran Melalui Dua Plat Datar

Fenomena aliran fluida pada umumnya dapat disimulasikan dengan menggunakan software CFD yang ada. Namun sebelum melakukan simulasi dengan software-software tersebut, sifat-sifat fisika dari aliran tersebut harus dianalisis terlebih dahulu, untuk menentukan parameter dan karakteristik yang terjadi pada aliran tersebut. Karakteristik aliran fluida tersebut akan berpengaruh nantinya pada penentuan kualitas grid yang akan digunakan saat simulasi. Hal ini dibahas dalam Grid Dependency Test, yaitu studi pengaruh kualitas grid terhadap hasil simulasi CFD.

Grid yang baik adalah grid yang dapat mewakili fenomena aliran seperti pada keadaan sebenarnya (yang mungkin mengalami perubahan secara cepat).

Metode Bisection

Metode Bisection merupakan salah satu metode iterative, dimana dalam metode ini digunakan dua nilai tebakan yang memiliki karakteristik dekat dengan nilai akar-akar sebenarnya.

Pada grafik di atas kita misalkan titik a adalah x₀ dan b adalah x₁, dimana jika dimasukkan dalam persamaan f(x), f(x₀) dan f(x₁) akan menghasilkan nilai yang berlawanan tanda. Kemudian kita melakukan ‘Bisect’, yaitu menentukan nilai tengah x₂ dari dua nilai tebakan tersebut, dengan persamaan :

x₂ = (x₀+x₁) /2

jika nilai f(x₂) = 0, maka nilai x₂ tersebut adalah akar dari persamaan tersebut. Jika f(x₂) > 0, maka akar terletak di antara x₀ dan x_2. Pada langkah iterative berikutnya, kita harus mengganti x1 dengan nilai x2.  Jika f(x₂) < 0, pada langkah iterative berikutnya, kita harus mengganti nilai x₀ dengan nilai x₂. Selanjutnya kita akan mencoba untuk menerapkan metode ini untuk mencari akar persamaan dari suatu fungsi polynomial.

Kita akan menggunakan contoh soal pada buku Computer Oriented Numerical Methods, halaman 38. Fungsi polynomial yang akan kita gunakan adalah x² – 25, dengan nilai tebakan awal x₀ = 2.0 dan x₁ = 7.0.

Algoritma Bisection :

1. Baca x₀,x₁,e. x₀ dan x₁ adalah 2 nilai estimasi awal terdekat pada nilai akar yang sebenarnya, e adalah nilai error yang diijinkan. Langkah 2,3 dan 4 merupakan step inisialisasi variable yang digunakan.

2. y₀=f(x₀)

3. y₁=f(x₁)

4. I =0

5. if(sign(y₀) = sign(y₁) kemudian

Mulai tulis “starting value unsuitable”

                        tulis x₀,x₁,y₀,y₁

            berhenti

6. While |(x₁ - x₀)/x₁| > e lakukan

        mulai

7.             x₂=(x₀+x₁)/2

8.             y₂=f(x₂)

9.             i=i+1

10.           if(sign(y₀) = sign(y₂) kemudian x₀=x₂ else x₁=x₂

       Berhenti

11. tulis “sollution converges to a root”

12. tulis “number of iteration =  “,i

13. tulis x₂,y₂

14. berhenti

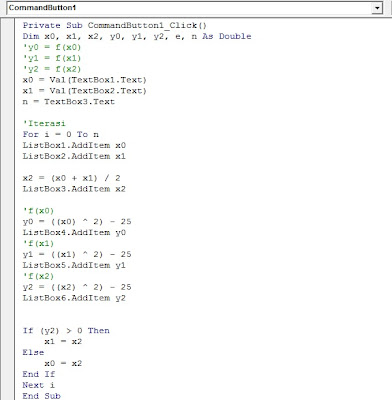
Berikut adalah penerapannya dalam Program Visual Basic.

Gambar 1. User Form

  

 

Gambar 2. Koding Bisection Method

Gambar 3. Hasil Iterasi

Dengan menentukan nilai estimasi awal xo = 2 dan x1 = 7 dan jumlah iterasi adalah 100, maka untuk fungsi y = f(x) = x² – 25, didapatkan akar-akar yaitu x = 5.

Metode Iterative

Metode iteratif adalah suatu metode untuk menyelesaikan suatu sistem persamaan baik persamaan tersebut merupakan persamaan linear maupun fungsi polynomial, trigonometi, dan exponensial dengan cara tidak langsung. Metode iteratif dimulai dengan aproksimasi nilai tebakan awal untuk mendapatkan solusi yang sebenarnya dengan melakukan perhitungan yang diulang-ulang (looping) sampai ketelitian yang diinginkan, sampai didaptkan hasil yang konvergen, yaitu hasil aproksimasi terdekat dari persamaan tersebut.

Metode Iterative terdiri dari beberapa macam, diantaranya:
1. Metode Bisection
Metode Bisection ini didasarkan pada teorema nilai antara fungsi kontinyu, yaitu bahwa suatu selang [x₀,x₁] harus mengandung f(x) = 0, bila f(x₀) dan f(x₁) berlawanan tanda. Proses dilakukan dengan pengulangan membagi selang [x₀,x₁] menjadi dua dan dalam setiap langkah diambil setengah selang yang memenuhi persyaratan tersebut. Proses ini diulang sampai didapatkan ketelitian yang sama dengan interval [x₀,x₁] terakhir. Kelebihan metode ini adalah kepastian untuk tercapainya konvergensi, sehingga didapatkan nilai akar-akar yang diinginkan. Namun kekurangannya adalah untuk mendapatkan nilai akar-akar sebenarnya, mungkin dibutuhkan jumlah pengulangan yang cukup banyak.

2. Metode False Position
Solusi akar-akar dengan menggunakan Metode False Position merupakan modifikasi dari Metode Bisection dengan cara memperhitungkan ‘kesebangunan’ yang dilihat pada kurva berikut:

Dari kesebangunan 2 segitiga  PCB dan  PQR pada gambar tersebut, maka kita akan mendapatkan persamaan :

PB/BC = PR/RQ

(F(b) -0) / (b - c) = f(b) – f(a) / (b - a)

Sehingga :

c = b – f(b)[(b – a)/(f(b) – f(a))]

Kelebihan dari metode ini adalah kepastian untuk tercapainya konvergensi sama seperti metode bisection. Kelemahannya, metode ini sangat sensitive dengan nilai tebakan awal dan untuk mencapai konvergensi mungkin membutuhkan iterasi yang cukup banyak.

3. Metode Newton-Raphson

Metode Newton Raphson adalah metode iterasi lain untuk memecahkan persamaan f(x) = 0,dengan f diasumsikan mempunyai turunan kontinyu f’. Metode ini menggunakan suatu garis lurus sebagai hampiran fungsi pada suatu selang. Garis tersebut adalah garis singgung kurva. Dengan menggunakan nilai awal x₀ dan kita tetapkan x₁ adalah titik potong antara sumbu x dengan garis singgung pada kurva f di titik x₀.

Prosedur metode Newton-Raphson mulai dari sebarang titik x₀ yang cukup dekat dengan akar. Pertama temukan kemiringan dari fungsi f(x) pada x-x₀, yang diberinama f’(x_o). Lalu tentukan x_i dengan persamaan

xi = x₀ – f(x₀) / f’(x₀)

Untuk setiap iterasi ke (i+1), hitung :

x_i+1 = x_i – f(x_i) / f’(x_i)

Kelebihan metode ini adalah hanya dibutuhkan satu buah nilai tebakan. Jika nilai tebakan tersebut berada dekat dengan nilai akar sesungguhnya, maka hanya dibutuhkan jumlah iterasi yang sedikit. Kekuranganya, dibutuh jumlah iterasi yang cukup banyak jika nilai tebakan berada jauh dari nilai akar aslinya.

4. Metode Secant

Dalam setiap iterasi untuk metode Newton-Raphson dilakukan perhitungan turunan fungsi atau f’(x). Metode secant menghampiri turunan pertama fungsi dengan :

f’(x) = (f(x_i) – f(_xi-1)) / (x_i – x_i-1)

dimana x_i dan x_i-1 adalah dua hampir akar untuk iterasi ke-I dan iterasi ke-(i-1). Nilai hampir akar pada iterasi ke-(i-1) diperoleh dari dua nilai hampir akar sebelumnya yaitu x_i-1 dan x_i yang diterapkan pada persamaan tersebut :

x_i+1 = (x_i-1 f(x_i) – x_if(x_i-1)) / f(x_i) – f(x_i-1)

dengan x_i-1 adalah absis titik perpotongan garis lurus yang menghubungkan dua titik (x_i-1,f(x_i-1)) dengan (x_i, f(x_i)).

5. Metode Successive Approximation

Metode Finite Volume pada Fenomena Diffusi-Konveksi

Fenomena Diffusi-Konveksi dapat diselesaikan dan dijelaskan dengan menggunakan metode Finite Volume. Sebelumya, kita harus mengetahui contoh-contoh peristiwa diffusi konveksi. Perisitiwa konveksi merupakan peristiwa perpindahan molekul fluida yang dapat disebabkan akrena adanya penambahan atau pegurangan panas. Contohnya adalah jika suatu batang logam yang dipanaskan kedua ujungnya pada temperature tertentu, maka akan terjadi rambatan panas secara konduksi pada batang logam tersebut. Bagian batang logam yang bersentuhan dengan udara akan menerima rambatan panas tersebut. Kemudian panas tersebut akan merambat pada udara, yaitu dengan cara konveksi.

Skema-skema yang dapat digunakan dalam menyelesaikan penomena konveksi, antara lain :

1. Central Differencing
2. Upwind Differencing
3. Hybrid Differencing
4. Power Law
5. Higher Order Differencing Sceme => Quadratic Upwind Differencing Sceme (QUICK)

Penyelesaian Persamaan Aljabar Simultan dengan Visual Basic

Pada posting sebelumnya, kita telah mencoba membahas tentang penyelesaian aljabar simultan dengan menggunakan metode Gausian yang dibantu dengan excel. Sekarang kita akan mencoba menyelesaikan persamaan aljabar dengan 5 persamaan dan 5 variabel tidak diketahui dengan metode Gausian dengan menggunakan Visual Basic.

Persamaan aljabar dengan 5 persamaan dan 5 variabel tidak diketahui, memiliki bentuk sebagai berikut :

a₁₁x₁   + a₁₂x₂   +a₁₃x₃ + a₁₄x₄  + _a15x₅              = a₁₆

a₂₁x₁   + a₂₂x₂   +a₂₃x₃ + a₂₄x₄  + _a25x₅              = a₂₆

a₃₁x₁   + a₃₂x₂   +a₃₃x₃ + a₃₄x₄  + _a35x₅              = a₃₆

a₄₁x₁   + a₄₂x₂   +a₄₃x₃ + a₄₄x₄  + _a45x₅              = a₄₆

a₅₁x₁   + a₅₂x₂   +a₅₃x₃ + a₅₄x₄  + _a55x₅              = a₅₆

Untuk melakukan langkah selanjutnya, untuk setiap indeks a, kita menggunakan indeks aij dimana i menentukan urutan baris dan j menentukan urutan kolom. Algoritma yang digunakan adalah sebagai berikut :

1. Untuk i = 1 sampai 5 dan j = 1 sampai 6, baca i dan j sebagai aij;
2. Untuk i = 2 sampai 5 dan j = 1
   Uij = ai1/a11
3. Untuk i = 2 samapi 5 dan j = 1 sampai 6
   aij = aij - ui1 x aij
4. Untuk i = 3 sampai 5 dan j = 2
   Uij = ai2/a22
5. Untuk i = 3 samapi 5 dan j = 2 sampai 6
   aij = aij - ui2 x aij
6. Untuk i = 4 sampai 5 dan j = 3
   Uij = ai3/a33
7. Untuk i = 4 samapi 5 dan j = 3 sampai 6
   aij = aij - ui3 x aij
8. Untuk i = 5 dan j = 4
   Uij = ai4/a44
9. Untuk i = 5 dan j = 4 sampai 6
   aij = aij - ui4 x aij

Dengan menggunakan Microsoft Visual basic, maka algortima tersebut akan dituliskan menjadi berikut :

Gambar 1. Koding

 Gambar 2. UserForm

Gambar 3. Hasil Simulasi

Demikianlah contoh penyelesaian persamaan aljabar dengan 5 persamaan dan 5 variabel tidak diketahu. Semoga bermanfaat. :-)

Persamaan Aljabar Simultan

Persamaan Aljabar yang harus diseleswaikan secara simultan, dapat dikerjakan dengan menggunakan metode Gausian, yaitu dengan menggunakan metode eliminasi. Berikut adalah algoritma untuk melakukan alkulasi ini.
Persamaan aljabar tersebut kita susun ke dalam bentuk matriks untuk mempermudah langkah selanjutnya.

Gambar 1. Matrix Awal (Sesuai dengan Persamaan).

1. Eliminasi a21 dengan step sebagai berikut :
   1. For i =1 to 3 dan j = 1 to 4 in step of 1 do read aij endfor
   2. for 1 = 2 to 3 in step of 1 do
   3.     u = ai1/a11
           'u = a21/a11
   4. for j = 1 to 4 in step of 1 do
   5.     aij = aij - u a1j
           a21 = a21 - u a11
2. Setelah kita membut algoritma tersebut, maka kita akan mendapatkan hasil sebai berikut. Pada kesempatan kali ini, kita mencoba mengerjakan algoritma tersebut dengan menggunakan microsoft excel.

   

   Gambar 2. Perhitungan dengan Menggunakan Excel
3. Penjabarannya adalah sebagai berikut :
   untuk mendapatkan nilai a2j yang baru, step-step yang terjadi berdasarkan algoritma pada point 1 adalah :
      u = a21 / a11
   step 5 -> a21 = a21 - u a11 ; a22 = a22 - u a12; a23 = a23 - u a13; a24 = a24 - u a1
      u = a31 / a11
   
     
   
   
   
   
   
   

Simulasi Konveksi Aliran Laminer Akibat Perbedaan Tempratur

Pada kesempatan kali ini, kita akan mencoba melihat pola aliran udara pada suatu ruangan yang disebabkan adanya perbedaan tempratur pada dinding ruangan tersebut tanpa celah inlet  dan outlet.

Langkah-langkah dan analisanya adalah sebagai berikut :

1. Atur Domain dengan Dimensi 1x1 m dan jumlah cell 10x10.
2. Kemudian kita melakukan edit cell. Seperti yang ditunjukkan pada gambar 1, kita mendefinisikan 2 jenis dinding yang berbeda yaitu W1 dan W2 dimana kedua dinding ini memiliki tempratur yang berbeda.
3. Input Konstanta Sepadan dan Kosntanta Fisikal. Pada command ini, kita mendefinisikan bahwa W1 memiliki tempratur 273 K dan W2 memiliki tempratur 313 K.
4. Input Mahir. Pada command ini, kita mendefinisikan adanya gaya grafitasi yang nantinya akn berpengaruh pada aliran udara dalam ruangan tersebut. Berikut adalah teori singkatnya.
   Massa jenis udara akan mengalami penurunan ketika udara tersebut diberikan perlakuan panas. Udara yang memiliki tempratur lebih tinggi akan cenderung bergerak naik ke atas yang disebabkan massa jenisnya lebih kecil dibandingkan massa jenis udara dengan tempratur lebih rendah. Pergerakan udara panas tersebut ke atas disebabkan desakan dari udara lainnya yang ada di sekitarnya. Aliran udara tersebut disebut dengan aliran konveksi laminar. Untuk  mendukung teori tersebut, kita akan melihat hasil simulasi pada gambar 2 di bawah ini.

   

   Gambar 1. Grid

Gambar 2. Pola Aliran Konveksi Udara di Dalam Ruangan

Dari pola kecepatan aliran udara pada gambar di atas, kita mengetahui bahwa udara di atas W2 cenderung bergerak naik ke atas sesuai dengan teori yang telah di jelaskan di atas, dan ruang kosong tersebut akan terisi oleh udara yang berada di sampingnya, yang menyebabkan aliran konveksi tersebut. Demikian hasil simulasi ini. Selanjutnya kita akan mencoba melihat pola aliran udara pada kamar tidur dimana terdapat perbedaan tempratur pada dinding-dinding kamar tidur tersebut. Semoga bermanfaat.